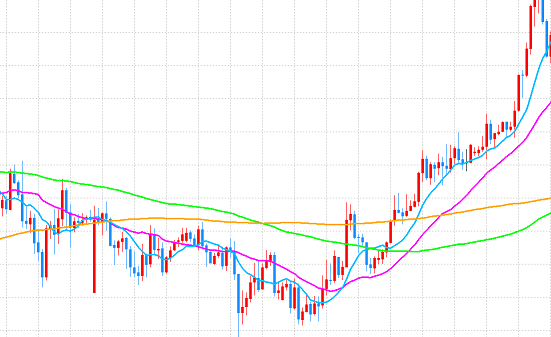
【FX】その線の意味、知ってる？｜チャートのテクニカル指標の紹介（移動平均線編）- お金の種

みなさん、FXでチャートを表示する際、ローソク足とともに、チャート上、もしくはチャート下部にいろいろな線を表示させている方もいらっしゃると思います。

今回は、チャートに表示されるテクニカル指標で最も有名な、移動平均線について、解説していきます。

移動平均線の種類

最近は、よくニュースでも、新型コロナ患者数の推移として、1週間移動平均などで使われておりますので、耳にしたことがあるというう方も多いかと思います。
_{※ちなみに、新型コロナ患者数の推移で使用している移動平均は、単純移動平均です。}

実は、この移動平均線、多数開発されていますが、今回は、以下の４種類の移動平均線について解説していきます。

単純移動平均線（Simple Moving Average=SMA)
指数平滑移動平均線（Exponential Moving Average=EMA）
平滑化移動平均線（SMoothed Moving Average=SMMA)
線形加重移動平均線（Linear Weighted Moving Average=LWMA)

それぞれについて解説していきます。

単純移動平均線
（Simple Moving Average=SMA)

「単純」とあるだけあって、単純に対象期間の平均値を算出していきます。

計算方法は以下の通りです。

SMA[0]＝（cp［0］+cp［1］+cp［2］+　…　+cp［n-1］）／n

n　　　：対象期間
cp［0］：現在の終値
cp［1］：1つ前の終値
cp［2］：2つ前の終値
…
cp［n-1］：n-1個前の終値　_{※一般的に、終値を使用されます。}

例えば、ドル円1時間足の2021年3月25日4:00における、5期間の単純移動平均を算出するすると、以下の通りとなります。

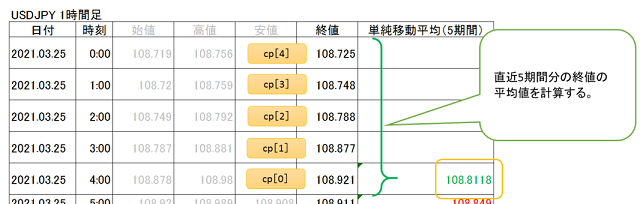
SMA[0]＝（cp［0］+cp［1］+cp［2］+cp［3］+cp［4］）／5
　　　　＝（108.921+108.877+108.788+108.748+108.725）／5
　　　　＝108.8118

そして、時間経過とともに、使用する5期間の終値もずらしていくことで、移動平均の算出値も変化していきます。

この、移動平均の算出値を折れ線グラフでつなぎ合わせたものが、移動平均線となります。

以降紹介する各移動平均についても、算出方法は異なりますが、最終的なグラフ化としては同じ方法で行います。

指数平滑移動平均線
（Exponential Moving Average=EMA）

「指数関数」と聞けば、昔、数学で聞いたことあるような…でも覚えてねぇ～という方も多いかと思います＾＾；

ですが、実際の計算には、指数は出てきませんので、ご安心くださいｗ

この指数平滑移動平均線が開発された意図としては、単純移動平均線では、期間内の価格変動は同等に取り扱うのに対し、直近の価格の影響度を大きく、過去にさかのぼるにつれて影響度を小さくすることで、直近の価格変動に応じて移動平均の反応を早くすることを目的としています。

計算方法は以下の通りです。

EMA[0]＝EMA[1]+{2/(n+1)}×(cp[0]-EMA[1])

n　　　：対象期間
cp［0］：現在の終値
EMA［1］：1つ前の指数平滑移動平均

例えば、ドル円1時間足の2021年3月25日4:00における、5期間の指数平滑移動平均を算出すると、以下の通りとなります。

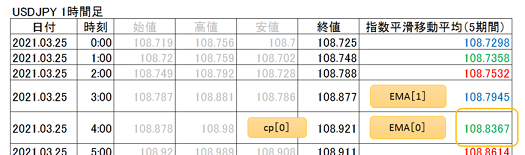
EMA[0]=EMA[1]+{2/(n+1)}×(cp[0]-EMA[1])
　　　　＝108.7945+{2/(5+1)}×(108.921-108.7946)
　　　　＝108.8367

この計算式で、直近のEMAから、現在の終値を用いて計算する必要がありますが、一番最初のEMAの値はどうするのか？という疑問が残りますが、一般的には、一番最初のEMAの値は、単純移動平均の値を用います。

また、指数平滑移動平均の期間の扱いですが、例えば5期間で算出しても、6期間以上前の数値も影響は残ります。

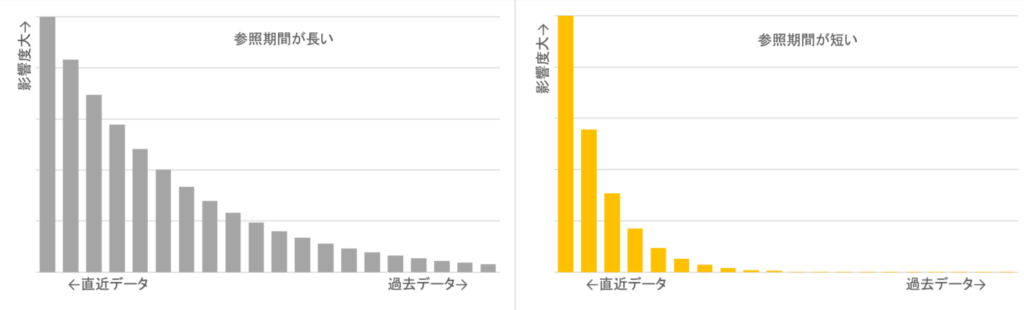
参照期間が長いと、過去データの影響度合いが大きく残り、参照期間が短いと、過去データの影響度合いが小さくなるというイメージで覚えておく程度で問題ありません。

いちおう、計算式は書きましたが、いまは計算せずともにチャートに表示することは可能ですので、ざっくりと、「指数平滑移動平均は、直近の終値の影響を大きくした移動平均」ぐらいで覚えておけばいいと思います。

平滑化移動平均線
（SMoothed Moving Average=SMMA)

次は、「平滑化」「Smoothed=スムース」ということで、なんとなくのぺーっとしてくれそうな移動平均かなーと感じてもらえますでしょうかｗ

開発された意図としては、価格急変のノイズの影響を低減させることで、トレンドの方向性を見極めるために使いましょうということのようです。

指数平滑移動平均とは逆のイメージですね。

計算方法は以下の通りです。

SMMA[0]＝{SMMA[1]×(n-1)+cp[0]}／n

n　　　　　：対象期間
cp［0］　　：現在の終値
SMMA［1］：1つ前の平滑化移動平均

例えば、ドル円1時間足の2021年3月25日4:00における、5期間の平滑化移動平均を算出すると、以下の通りとなります。

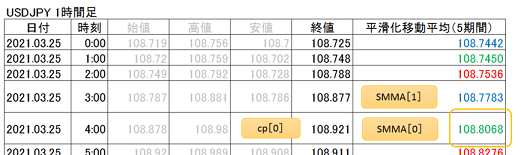
SMMA[0]={SMMA[1]×(n-1)+cp[0]}／n
　　　　＝{108.7783×(5-1)+108.921}／5
　　　　＝108.8068

この計算式でも、EMAと同様、直近のSMMAと、現在の終値を用いて計算する必要がありますが、一番最初のSMMAの値は、単純移動平均の値を用います。

この平滑化移動平均についても、常にひとつ前のSMMAの値を用いるため、参照期間以前の価格の影響も残ります。

また、直近価格の影響度は、単純移動平均と同じ影響度しかないため、参照期間以前の価格の影響を受けている分だけ、単純移動平均よりも平滑化されることとなります。

こちらも当然、計算せずともにチャートに表示することは可能ですので、ざっくりと、「平滑化移動平均は、急変ノイズを平滑化した移動平均」ぐらいで覚えておけばいいと思います。

線形加重移動平均線
（Linear Weighted Moving Average=LWMA)

「線形加重移動平均」…かたっ苦しい単語が並んでいます＾＾；

この、線形加重移動平均も、指数平滑移動平均と同様、直近の価格の影響度を大きく、過去にさかのぼるにつれて影響度を小さくすることで、移動平均の反応を早くすることを目的としています。

その加重の掛け方について、線形で加重をかけることを特徴としている移動平均です。

例えば、参照期間5のEMAとLWMAの影響度は以下のような形となります。

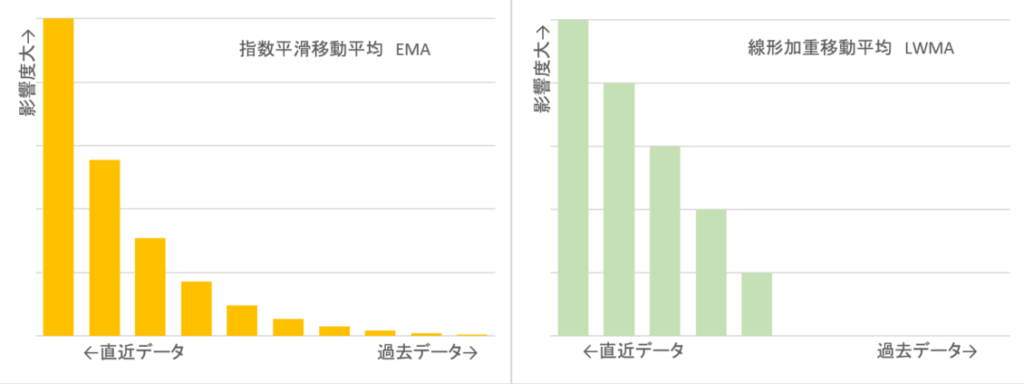
いずれも、直近データの影響度が大きく、過去データになるにつれて影響度は小さくなりますが、指数平滑移動平均の場合は、少しではありますが過去にさかのぼって価格の影響はありますが、線形加重移動平均の場合は、過去データにさかのぼるにつれ影響度は直線的に減少していき、参照期間を外れると全く影響しないことを特徴としています。

計算方法は以下の通りです。

LWMA[0]＝〔cp[0]×n + cp[1]×(n-1) + cp[2]×(n-2) + … + cp[n-1]×{n-(n-1)}〕
／〔n+(n-1)+(n-2)+ … +{n-(n-1)}〕

n　　　：対象期間
cp［0］：現在の終値
cp［1］：1つ前の終値
cp［2］：2つ前の終値
…
cp［n-1］：n-1個前の終値

例えば、ドル円1時間足の2021年3月25日4:00における、5期間の線形加重移動平均を算出する場合は、

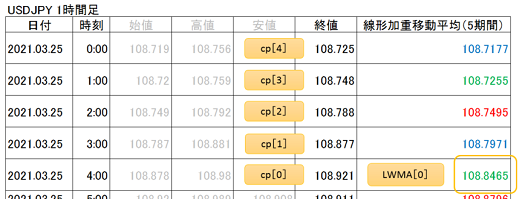
LWMA[0]＝〔cp[0]×n + cp[1]×(n-1) + cp[2]×(n-2) + … + cp[n-1]×{n-(n-1)}〕
　　　　　　／〔n+(n-1)+(n-2)+ … +{n-(n-1)}〕
　　　　＝（108.921×5 + 108.877×4 + 108.788×3 + 108.748×2 + 108.725×1）／（5+4+3+2+1）
　　　　＝108.8465

それぞれの移動平均線を比較

今回紹介しました、移動平均線が、どのような動きになるのか、チャートの一部を切り取って確認してみます。

ピンク：SMA(10)　ブルー：EMA(10)
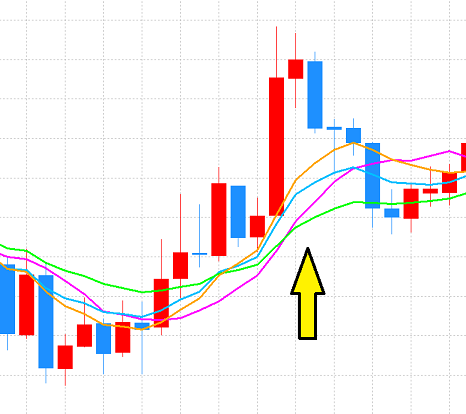
グリーン：SMMA(10)　オレンジ：LWMA(10)

全て参照期間を10として、急変動があった時に、それぞれどのような動きになるのか比較します。

SMA　：価格上昇に伴って、SMAの線も上昇している。
EMA　：SMAと比較し、価格上昇に伴い、素早くEMAの線も上昇、その後、下降に転じた際も、SMAは
　　　　まだ上昇しているのに対し、EMAは下降している。
SMMA：価格上昇に伴って、SMMAの線も上昇はしているが、SMAと比較して反応は遅い。
LWMA：EMAと同じく、価格上昇に伴い、素早くLWMAの線も上昇、下降に転じた際も、LWMAの線も
　　　　下降している。
　　　　EMAと比較しても、反応が早い。

それぞれの移動平均のところで開発意図をかきましたが、おおむね意図した通りの動きとなっていることがわかります。

上記のような特徴があることを理解したうえで、活用いただければと思います。